Next, we will derive the proportionality relationships for the above equations, using boundary conditions (i.e. mass of the star at radius R is the mass of the sun, temperature of the star at radius 0 is the central temperature, etc.). For this derivation, we will replace the differentials with deltas, i.e. "change," since we are only interested in proportionalities.
For the first equation, we have:
i.e. Pressure is proportional to the mass of the star times the density, divided by the radius of the star.
We will skip the second equation (radiative diffusion) for now. The third equation gives us:
i.e. The mass of the star is proportional to its radius cubed multiplied by the density.
The fourth equation gives us:
i.e. Temperature is proportional to pressure divided by density.
Let's combine our results to get a useful relation for the central temperature of a star. We know that:
where M is the mass of the star and a R is the radius of the star.
Using our results, we have:
Thus, the central temperature of a star is proportional to its mass divided by its radius.
Now we will derive the relations of stellar structure for a star on the main sequence (i.e. a star steadily fusing hydrogen, implying a constant core temperature T_c = constant).
For the mass/radius relationship, we have:
Hence, a star on the main sequence has a radius proportional to its mass.
To derive the luminosity/mass relationships, we look back at our radiative diffusion equation, and find that:
For a medium-mass star, we take kappa to be constant (this is because electron scattering plays the dominant role in determining the value of kappa, making is essentially constant). Hence:
Thus, the luminosity of a medium-mass star scales with the third power of its mass.
For a low-mass star, kappa is no longer constant. Instead, we have:
So, the luminosity/mass relationship becomes:
Thus, the luminosity of a low-mass star scales with the fifth power of its mass.
Now we will find the relationship between luminosity and temperature (effective temperature, not the temperature of the core).
For a medium-mass star, we have:
We also know that luminosity is related to radius and temperature by the following:
Hence, we have:
This is the luminosity/temperature relationship for a medium-mass star.
For a low-mass star, we have:
This gives us the Hertzsprung-Russell (HR) diagram: if we plot luminosity versus temperature on a log-log graph, we have:
i.e. a the log-log plot is linear. (for low-mass stars, the plot is also linear, with a gentler slope)
The HR diagram looks something like this:
Here is an actual HR diagram, using empirical data. You can see that for stars on the main sequence, the luminosity/temperature relationship is (roughly) linear on a log-log scale:

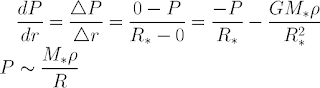










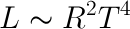




No comments:
Post a Comment