Convert the units of the blackbody intensity from Bv(T) to Bλ(T). IMPORTANT: Remember that the amount of energy in a frequency interval dv has to be exactly equal to the amount of energy in the corresponding wavelength interval dλ.To start off, we need the expression for Bv(T):
The question is asking to convert Bv(T) to Bλ(T). Mathematically, we can relate frequency to wavelength by:
So, it makes sense to use the above relation to substitute frequency with the speed of light divided by wavelength, right?
WRONG. I made the same mistake when I first did this problem. If you look at the hint, it says to remember energy. Substituting v with (c/λ) doesn't change the physical meaning of Bv(T) - the energy per area per second per frequency emitted by a blackbody. Substituting out frequency will *not* change the units, and Bv(T) will still give you the energy corresponding to a certain frequency, instead of a certain wavelength, which is what we want.
So how do we solve this problem? Consider the two (qualitative) plots of Bv(T) and Bλ(T):
Why is this true? Remember that B(T) is the metric describing the amount of energy per area per time per quantity related to light. This quantity can be wavelength *or* frequency. In other words, Bλ(T) describes the energy emitted by a blackbody associated with a specific wavelength, and Bv(T) describes the energy emitted by a blackbody associated with a specific frequency. Each of these functions multiplied by a differential of the associated quantity (small enough that the energy remains constant over such a small interval) must be equal to each other, as expressed by the above relationship. Now we can solve for Bλ(T):
To find dv/dλ, we can differentiate our previous relationship:
We can drop the negative sign because we are only concerned with the magnitude of our answer (after all, the energy emitted must be positive). Plugging into our original equation and substituting out frequency, we get:






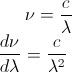

Good post. Check the shape of your plots. B_lambda should have the same overall shape, but since Bnu exponentially declines toward high frequencies, Blambda must decline exponentially toward *short* wavelengths. See Ellen's writeup.
ReplyDelete