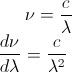Estimating the Luminosity of the Sun using a 60W Lightbulb

In this post I'll be doing problem #2 from this week's worksheet on stellar properties. I chose this problem because it used a crucial concept of physics to answer a fun and extremely entertaining question. Here's the problem:

Use a 60 Watt light bulb to estimate the luminosity of the Sun. How does your value compare to the actual value?

That's the entire question. Use a light bulb to estimate the luminosity of the Sun. Where would one even begin?

It's actually quite simple. You need to only use a light bulb to find the Sun's luminosity - that means you need to measure some quantity that is the same for the light bulb and the Sun. That quantity turns out to be the power absorbed by your hand.

Think about it like this: on a hot summer day, you can walk outside and stretch out your hand. The rays of light from the Sun will be absorbed into your hand, and you will feel a "heat" that is caused by the Sun, not by the air temperature. If you hold your hand close to a light bulb, you will feel a similar sensation. This sensation is the power, or energy absorbed by your hand per second. So, we have:

Now, we're given the power output of the bulb. How can we relate that to the power output (luminosity) of the Sun? We need to somehow relate the power output of the bulb with the power absorbed by your hand. We can use Gauss's Law for light intensity to find this. Because of conservation of energy, the amount of energy outputted by a source of light per time (i.e. power) is the same on any surface enclosing the source. In other words, if you surround a light bulb with a shell of radius R, that shell will absorb the same amount of energy as a shell of radius 2R.

For the purposes of this problem, it will be convenient to surround our light bulb with an imaginary spherical shell with a radius equal to the distance from your hand to the center of the light bulb (the distance at where you feel the same heat on your hand as you do on a hot summer day). Because a sphere is rotationally symmetric, the power absorbed at any point on the sphere is the same. So, we can express the power absorbed by your hand as a fraction of the power output of the light bulb. Thus, we can write:

We know from before that the power absorbed by your hand is the same for the Sun's case. Except in this scenario, the distance from your hand to the Sun is an astronomical unit (AU)! That's about 1.5 x 10^13 cm. So for the Sun:

Equating the two, we have:

The distance between your hand and the bulb will be around 10cm, so:

The actual luminosity of the sun is 3.839x10^33 ergs/second, so we're within an order of magnitude to the correct answer!

Hubble's Law - A Simulation

I recently found a cool simulation on the web that interactively demonstrates Hubble's Law. You can create and destroy galaxies, change the value of Hubble's Constant, and watch things unfold. The link is here:

http://carma.astro.umd.edu/AWE/deploy/Hubble.html

Pretty cool stuff!

Young's Double Slit Experiment - Brightness Patterns

In this post I'll be doing #1a from this weeks worksheet on optics. I chose this problem because it let me familiarize myself with optics and why Fourier transforms are used in the field. I struggled particularly hard on this concept and working through this problem helped me understand the ideas in the worksheet better. Here's the problem:

Convince yourself that the brightness pattern of light emerging from the two slits as a function of angle is a cosine function, and that the brightness pattern on the screen is the square of this function.

The two slits refer to the two slits used in Young's double slit experiment, and the screen is the sheet that the light passing through the two slits is projected onto. Here's a picture showing the setup:

(from Wikipedia)

In this setup, we assume L to be much greater than d. So, how do we determine that the brightness pattern on the screen is the square of a cosine function of angle?

First, let's talk about diffraction and interference. Light diffracts, so upon entering the slit, the incident light will spread out in all directions. Light also interferes, so if light from one slit hits a spot, it will interfere with the light from the other slit in a way that depends on the relative phases of the two light waves.

Looking at the above diagram, we have light drawn from the two slits to the same arbitrary point. Since L is much greater than d, we can assume that the two rays of light are essentially parallel near the slits. So, we can modify the diagram as follows:

Since the distance between the screen and the slits is so large, we can effectively say that the distance from the bottom slit to the arbitrary point is equal to the distance from the top slit to the point plus some "extra" bit x. Using trigonometry and a small angle approximation (which we can do, since d is much smaller than L), we have:

So, what is x? Let's think about interference. Constructive interference is when two waves add together in the same phase. In other words, the extra distance that the ray from the bottom slit travels must be equal to an integer multiple of the wavelength of light - then the two rays will be "in phase" at the point on the screen:

What about destructive interference? Our two rays of light will interfere destructively when they produce a brightness of zero - thus, they must be out of phase by half a wavelength:

This means that points of maximum brightness on our screen our spaced apart with a distance of the wavelength of light divided by the distance between the two slits, and points of zero brightness are spaced apart with the same distance, exactly in between the brightest spots. Thus, our brightness pattern is a periodic function that is continuous, since the light rays are continuous waves. At an angle of zero, exactly in between the two slits, we obviously get constructive interference (since the waves travel the same amount), so there must be a maximum at the zero. This is described perfectly by the cosine function.

I'm actually mildly incorrect. The cosine function describes the electric field of the two light rays, not the intensity on the screen. Intensity is actually the square of the electric field, so our brightness pattern at the screen is really a cosine squared function.

It turns out that this behavior is described by the Fourier Transform, which makes it extremely useful to use the Fourier Transform when talking about optics in astronomy. 

Olbers' Paradox

Why is the sky dark at night?

This was a question that German astronomer Heinrich Wilhelm Olbers described in 1823. If the universe were static and infinite, then the night sky should be incomparably bright, as the light from an infinite number of stars would fill the horizon. The dimness of stars farther away would be countered by the fact that there would be more stars farther away from us (assuming a near-constant density of stars).

Of course, the paradox is resolved by a number of explanations. Here are a few:

• The universe has only a finite number of stars
• The distribution of stars is not uniform (e.g. many could be blocked by others stars)
• The universe is expanding
• The universe is young, so distant light hasn't reached us yet

Nevertheless, the sheer simplicity of Olbers' Paradox is profound. A dark night sky is something that we all take for granted, yet the darkness itself imposes certain restrictions on the universe.

A more detailed overview of Olbers' Paradox can be found on Wikipedia:
http://en.wikipedia.org/wiki/Olbers'_paradox

The Rayleigh-Jeans Tail

In this post I'll be doing #2d from this week's worksheet on blackbody radiation. I chose the problem because it transforms an ugly equation into a nice relationship using approximations, illustrating the importance of approximations and ballpark mathematics in astronomy. Here's the problem:

Let's consider photon energies that are much smaller than the thermal energy. Use a first-order Taylor expansion on the term e^(hv/kT) to derive a simplified form of Bv(T) in this low-energy regime. Radio astronomers like to talk about the "brightness temperature" of an object, rather than its actual brightness. Why do you suppose they talk about temperatures instead of intensity, like normal people?

Let's start with the expression for Bv(T):

A messy equation, indeed. However, we are concerned with photon energies that are much smaller than thermal energies:

With this assumption, we can Taylor expand the term on the denominator:

Since this is astronomy, let's not worry about higher order terms and focus on the first-order approximation:

Substituting into our original equation:

Thus, using our approximations, we have shown that Bv(T) has a linear relation with temperature!

Now the second part of the question. Why do radio astronomers talk about the "brightness temperature" of an object? Looking at our above expression, the answer is evident. Since the intensity of a blackbody is proportional to temperature, we can immediately know one of them, given the other! In other words, describing a blackbody at low energies with its temperature is equivalent to describing its intensity.

(Note: this still doesn't mean that radio astronomers are normal people...:) )

The Wien Displacement Law

In this post I'll be doing #2b from this week's worksheet on blackbody radiation. I chose it because it represents why understanding a problem conceptually is much more important than grunging through mathematics. Here's the problem:

Convert the units of the blackbody intensity from Bv(T) to Bλ(T). IMPORTANT: Remember that the amount of energy in a frequency interval dv has to be exactly equal to the amount of energy in the corresponding wavelength interval dλ.

To start off, we need the expression for Bv(T):

The question is asking to convert Bv(T) to Bλ(T). Mathematically, we can relate frequency to wavelength by:

So, it makes sense to use the above relation to substitute frequency with the speed of light divided by wavelength, right?

WRONG. I made the same mistake when I first did this problem. If you look at the hint, it says to remember energy. Substituting v with (c/λ) doesn't change the physical meaning of Bv(T) - the energy per area per second per frequency emitted by a blackbody. Substituting out frequency will *not* change the units, and Bv(T) will still give you the energy corresponding to a certain frequency, instead of a certain wavelength, which is what we want.


So how do we solve this problem? Consider the two (qualitative) plots of Bv(T) and Bλ(T):

The top plot is a graph of Bv(T) with respect to v, and the bottom plot is a graph of Bλ(T) with respect to λ. What the hint is saying is that the energy in an interval of dv *must* be the same as the energy in an interval of dλ. In other words, the following must be true:

Why is this true? Remember that B(T) is the metric describing the amount of energy per area per time per quantity related to light. This quantity can be wavelength *or* frequency. In other words, Bλ(T) describes the energy emitted by a blackbody associated with a specific wavelength, and Bv(T) describes the energy emitted by a blackbody associated with a specific frequency. Each of these functions multiplied by a differential of the associated quantity (small enough that the energy remains constant over such a small interval) must be equal to each other, as expressed by the above relationship. Now we can solve for Bλ(T):

To find dv/dλ, we can differentiate our previous relationship:

We can drop the negative sign because we are only concerned with the magnitude of our answer (after all, the energy emitted must be positive). Plugging into our original equation and substituting out frequency, we get:

Lecture: Fourier Transforms

I just watched the lecture Melodie posted on Fourier transforms. One thing I learned was the different kinds of telescopes - I had no idea that some telescopes used three mirrors. A thing I like about the lecture was that it didn't delve too deeply into mathematical "grunginess," keeping things simple. However, that ties into something I disliked, which was the fact that some things felt too rushed. For example, I didn't really get a clear understanding of the physical meaning of the Fourier transform in regards to telescopes, or why we use it. A better explanation of the system being discussed would have been nice, as well as a quick derivation of some Fourier transforms.

Measuring the Radius of the Sun

How does one measure the radius of the Earth using...the Sun?

The answer's quite simple, in theory. You'll need at least two people, a stopwatch,  and a clear view of the horizon.

Last Sunday, the class went on a trip to Santa Monica beach to put theory to practice. We split up into groups and attempted to calculate the radius of the Earth using only the sunset and stopwatches. My group consisted of myself, Ronnel, Andy, and Krishnan.

Here's how we did it. Consider the Earth, modeled as a sphere. Say you have two people, one located at the surface, and one located a height 'h' above the surface. Their views of the horizon (the line of sight tangent to the surface of the Earth) will thus be different:

By geometric analysis, you can easily find that the angle made between your different horizons corresponds to the angle made between radii drawn fromthe Earth to the points on the horizons where the line of sight is tangent to the Earth (see above diagram). Using simple trigonometry, we get:

How do we find theta? It's just the angle between the two horizons - therefore, if you measure the difference in time between sunset for both observers and multiply by the angular speed of the Sun across the sky, you've found it. So:

Combining both equations, you get:

So now we have an expression for R. Let's plug in some numbers. The Sun travels 180 degrees (across the sky) in twelve hours, so it's angular speed is:

When we measured the Sun, we took multiple measurements using 4 people located at different heights. Our best time difference was 25.2 seconds, for a height difference of 3.33 meters. So:

Plugging this all in, we have:

The actual radius of the Earth is about 6378km, so we're off about 69% percent - yikes! But at least we're correct to within an order of magnitude, which is all you can really expect with a measurement this crude.

Science!

Lecture: Blackbody Radiation

I just watched the lecture Melodie posted on blackbody radiation. I liked how the video did not go too deeply into the mathematics. An interesting fact I learned was that blackbodies are perfect emitters as well as absorbers. However, I felt that the video was a bit slow and I spaced out frequently while waiting for pictures to be drawn. Also, an outline of topics covered near the beginning would have been nice, as sometimes the video abruptly went to a topic or application without warning, and I was a bit lost. (upon a second watching, this problem didn't come up again.)

Is The Universe a Computer Simulation?

Is the universe a giant computer simulation? Could we possibly find out if it were?

Some theorists believe it may be soon possible to detect if the universe were a computer simulation. The reasoning goes as follows:
1) Using supercomputers, we can apply the laws of quantum chromodynamics to simulate a small scale region of space a few femtometers across (10^-15 meters). One could hypothesize that a much more powerful computer could simulate a whole universe of space.
2) A computer simulation would have to transform the continuous laws of physics onto a 3-dimensional lattice separated into discrete chunks. This discrete nature of a simulation should manifest in limits in certain properties - for example, there would be a cutoff in the spectrum of high energy particles.
3) Further consequences of this simulation would result in cosmic rays travelling preferentially along the axes of the lattice. This preference would be something we could theoretically measure.

An article describing the idea is found on technologyreview.com:
http://www.technologyreview.com/view/429561/the-measurement-that-would-reveal-the-universe-as/

Personally, I don't buy the article's metaphysical connotations. Scientifically, such a measurement as described would only indicate a directional preference of certain cosmic rays, perhaps revealing a physical phenomenon we don't yet understand. Extrapolating as far as to say that such data provides evidence for the universe as a simulation is a leap of faith, to say the least. Who's to say that an alien civilization's numerical simulation techniques would be the same as ours?

(Meta)physics aside, the article's an interesting read, at least. The idea that the universe could be a simulation is fascinating in itself, although the scientific consequences are (in my opinion) irrelevant.

Declination and Observations

In this post I'll be doing #4 from this week's worksheet on celestial coordinates and observations. I chose it because it's actually really simple, unless you overthink it like I did. For me, personally, the concept of celestial coordinates was very confusing, mainly because I tried too hard to visualize everything and spent too long challenging my own thought process, resulting in an obfuscation of a concept that was simple to begin with.

Here's the problem:

You are planning a space mission to observe a small area of the sky (maybe 2 sq deg) very deeply (meaning you're staring at the same spot on the sky for a long time) to make a catalog of faraway galaxies at visible wavelengths, say 550 nm. What declination range should you point your space telescope at so that ground telescopes in both the Very large Telescope (VLT) and the Keck Telescopes can follow up on the galaxies you discover? The declination range should be observable from all observatories for at least 6 months a year.

This question really just hinges on a solid understanding of what declination is. At first, I tried to visualize what the sky would look like from the VLT and the Keck Telescopes; that's probably the wrong way to go, though. It's much easier to view the problem from a third-person perspective, looking at the earth from outside, like this:

The black line on the earth is an observer - theoretically, its field of view is from horizon to horizon. In other words, it can see 90 degrees on each side of straight up. Viewed from an exterior perspective, it's much easier to see the relation between latitude of the observer and declination of your observed target. Consider an extreme point of this scenario - an observer at the equator. An observer at the equator would have a 180 degree field of view along the tangent to the surface of the Earth. So, an equatorial observer would see from declination -90 to +90 (in degrees; we are assuming the observer can see infinitely far, so the furthest he/she could see would be at +- 90 degrees):

An observer between the equator and the north pole, then, would see 180 degrees, shifted by their latitude. An a latitude of x, he/she would be able to see from (-90 + x) to (90 + x).

If the observer were in the northern hemisphere, however, the upper bound of (90 + x) is actually 90, since declination is only measured from -90 to 90 degrees. If you think about it, after some time has passed, the Earth will have rotated, so the (90 + x) declination that the observer has seen before has become (90 - x). Because of this, it makes more sense to measure declination from -90 to 90 degrees, eliminating the confusion of angles greater than 90 degrees.

Let's turn back to the problem at hand. The VLT is at a latitude of -24 degrees, and the Keck Telescopes are at a latitude of 20 degrees. The observable declinations of the VLT, then, range from (-90 - 24) to (90 - 24), or -90 degrees to 66 degrees. The Keck Telescopes could theoretically view declinations from (-90 + 20) to (90 + 20), or -70 degrees to 90 degrees. Declinations viewable from both, therefore, would lie in the intersection of these two ranges, or -70 degrees to 66 degrees. Since these bounds represent the limit of viewability, let's take a smaller intersection, say: -60 degrees to 56 degrees. The following diagram shows this scenario graphically:

So, this problem is actually fairly simple. The important part was to consider an observer located at an arbitrary latitude, diagrammed from a point outside the Earth. Trying to imagine this problem on the surface of the Earth causes headaches (at least it did for me), and is less efficient. What about the part about being observable for at least 6 months a year? It's actually a red herring; the declination range observable from a latitude remains constant throughout the year.

The Cheerio Effect

Most days (ifI wake up in time), I like to enjoy a breakfast of Honey Nut Cheerios. With Honey Nut Cheerios, as with many other breakfast cereals, a curious phenomenon occurs when the cheerios float in milk (unless you are one of the few that consume cereal without milk, with which I have no response other than sadness). I'm sure many of you are well-acquainted with this so-called "Cheerio" effect, at least qualitatively. It goes something like this:

When cheerios float in milk, they tend to aggregate together into large clumps. The effect is visibly akin to objects gravitationally attracting each other to form a mega-clump.

Today I wondered whether anyone had analyzed this system quantitatively, and lo and behold, a scientific paper on the "Cheerio" effect:
http://people.maths.ox.ac.uk/vella/Vella2005.pdf

Here's the abstract:
Objects that float at the interface between a liquid and a gas interact because of interfacial deformation and the effect of gravity. We highlight the crucial role of buoyancy in this interaction, which, for small particles, prevails over the capillary suction that is often assumed to be the dominant effect. We emphasize this point using a simple classroom demonstration, and then derive the physical conditions leading to mutual attraction or repulsion. We also quantify the force of interaction in some particular instances and present a simple dynamical model of this interaction. The results obtained from this model are then validated by comparison to experimental results for the mutual attraction of two identical spherical particles. We conclude by looking at some of the applications of the effect that can be found in the natural and manmade worlds.

Lecture: Celestial Coordinate Systems

I just watched the short video lecture Melodie posted on celestial coordinate systems. In it, I learned a new way to think of the zenith: as a vector antiparallel to the gravity force vector. This new interpretation made so much more sense than my previous understanding of the zenith as a line pointing overhead, and I was able to visualize it a lot easier. One thing that wasn't as clear was how exactly the stars' location relative to an observer changed throughout the year. A picture or diagram of a particular star from an observer's viewpoint throughout the year would have been helpful.

An Brief Introduction to Order of Magnitude Calculations

Order of magnitude calculations are an extremely useful tool when you want to make rough approximations to arrive at answers very quickly. In astrophysics, many measurements are not very precise, so order of magnitude calculations can provide a crude answer that is actually fairly accurate, since the degree of precision is not very high in the first place. In other disciplines, order of magnitude calculations are usually much quicker than precise calculations and can give you a rough ballpark estimate of things.

I'm going to do a quick order of magnitude problem to highlight their incredible power. Here's the question:

"The eye must receive ~10 photons in order to send a signal to the brain that says, 'Yep, I see that.' If you are standing in an enormous, completely dark cave and just barely discern a light bulb at a distance of 1 kilometer, approximately what is the power output of the bulb (assume the bulb is emitting light isotropically)?"

The first thing I'm going to do is a draw a (bad) picture. When dealing with problems like these, it's important to be able to visualize the scenario, making the subsequent calculations much more intuitive.

Pictured above is the light bulb, you, and d, the distance between the two objects (1km). Notice the circle with the light bulb in the center - this will be come important for solving the problem.

Necessary for this problem is the understanding of the relationship between light intensity and distance. It's similar to Gauss' Law for Electricity, by the fact that intensity from a point source follows an inverse square-law relationship. In other words, if you "surround" a source of light with a shell, the intensity of light "captured" by the shell is the same, regardless of its shape or size. For a spherical shell, each patch of shell of equal area will receive the same intensity of light, due to the spherical symmetry of the system. Mathematically, we can express it like this:

Where I is the intensity of light, and dA is the differential piece of area of the enclosing shell. More intuitively speaking, if you imagine a light bulb emitting light, the "density" of light will decrease as you move away from the bulb, since the light will be spreading out further. However, the "total" amount of light will stay constant, so if you enclose the bulb in a surface, it will collect a constant amount of light no matter its shape or size.

If we assume the light bulb is emitting light at a constant rate, the above equations hold for power output also. Now, how do we solve the problem?

We're given that the eye must receive 10 photons to "detect" light. If we imagine the light bulb to be surrounded by an imaginary spherical shell radius d=1km, the eye will be a tiny patch of that surface. Because of the above equations, we know that the power output of the light bulb times the area of the shell is constant; thus, we are allowed to arbitrarily choose this 1km radius shell. Since a spherical shell is radially symmetric (if you rotate it in any direction, it will still look the same), each patch of the shell of equal area must receive the same amount of power. Thus, we can state the following:

This is simply a proportion: the area of your eye divided by the total area of the shell is equal to the light power received by your eye divided by the total power output of the light bulb. If we solve for this total power, we have solved the problem. Thus:

So, if we can find the values of the three quantities on the right side of the above equation, we're good. Let's do that:

The area of the shell is simple. The spherical shell has a radius of 1km, or 1000m, so the surface area is:

For now, I'm going to leave everything in terms of variables, and plug in these numbers are the end. For the area of the eye, I'm going to estimate it as 1 square centimer:

The power received by the eye is a bit tricker. Using the definition of power, we can relate it to energy and time like so:

The energy received by the eye is the energy of 10 photons, the minimum number of photons the eye must receive to detect light. The energy of a photon is equal to Planck's constant times the speed of light divided by its wavelength. Because this light is visible, we will estimate its wavelength to be around 500nm:

(where n = 10 )

The length of time per reception of energy can also be determined. Most movies have a refresh rate of about 30 frames per second, and video games can operate on 60 frames per second. I can personally tell the difference between these frame rates, so I'll assume the refresh rate of the eye to be about 60Hz. So, each "frame" that your eye receives in this cave will contain the energy of 10 photons, and there are 60 frames per second. Thus:

We're almost done now. Plugging everything back into the equation, we get:

Let's plug in numbers now:

What's our answer? About 0.00003 watts. Does that make sense? Well, it's a light bulb in a pitch-black cave that you can barely see, so perhaps. More important is how we arrived at this answer - using just some physics and a few estimations, we arrived at an answer very quickly.

Introductions

Hello, I'm Jonathan, a current sophomore at the Caltech Institute of Technology in Professor' Johnson's AY 20 class (Basic Astronomy and the Galaxy). This will be my blog containing homework, pictures, facts, and overall cool stuff about space (and stuff).

This is a panoramic view of the near-infrared sky, showing locations of several objects in space. The long blue line in the bottom right shows the location of the Great Attractor, a location in intergalactic space with the mass of tens of thousands of Milky Ways. Tens of thousands of galaxies, our own included, are hurtling towards the Great Attractor at over 14 million miles an hour! In 1987, a team at Caltech discovered this motion of the Milky Way, and hypothesized that there must exist a very massive object at the location of the so-called Great Attractor. Because it lies behind the plane of our own galaxy, dust and stars from the Milky Way obscure our view of the Great Attractor, making it difficult to determine what it exactly is.

Why is astronomy cool? Because of awesome names like "The Great Attractor." I'm looking forward to the rest of this class so much.