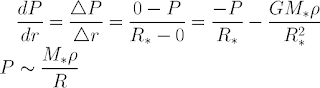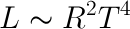Radial Velocity (Super-Fast) Lab(!)

In this post I'll be doing the Radial Velocity (Super-Fast) Lab handed out in class earlier this week. We're supposed to determine the period, mass, and semi-major axis of an exoplanet, given its host star's radial velocity curve. Here are the graphs (assuming a star's mass that is 1.5 times that of the sun):

The period is easy to determine by inspection. For the first graph, the period seems to be about 1 year. We can use Kepler's Third Law to determine the semi-major axis:

So:

To determine the mass of the planet, we can use the following equation:

where K, the amplitude of radial velocity, is expressed in fractional units using a constant (29.8 m/s), the mass of the sun, a period of a year, and the mass of Jupiter. For the first graph, we have an amplitude of about 100m/s. So, our mass is:

, where M_J is the mass of Jupiter.

What about the second graph? We can see that the radial velocity amplitude K is about 50m/s, and the period is roughly 3.3 years. The semi-major axis, therefore, is:

The mass of the planet is:

Exoplanets and Wobbly Stars

Exoplanets are planets found outside our solar system, and remain the focus of a rapidly growing field of astronomy. Detecting them, however, can be difficult, since they don't radiate light like stars, and are much smaller. In this post I'll be introducing the physics of one of the methods we use to detect exoplanets. The method utilizes the fact that exoplanets exert a gravitational force on their host star, resulting in a "wobbling" of the star as it orbits ever so slightly around the two bodies' center of mass.

Let's start from the basics. Consider a star and a planet, orbiting each other around their mutual center of mass:

The equation for the center of mass is:

In this case, we have set the center of mass to be at x=0. Substituting in our variables, we have:

Simplifying, we have the following relationship:

Thus, the distance from the star/planet to the center of mass is inversely proportional to its mass.

What can we do with this? We can use Kepler's Third Law to find out how much the Sun wobbles. Kepler's Third Law:

where a is the mean semimajor axis, the sum of a_p and a_*, and M is the sum of the mass of the star and the mass of the planet. If we assume the mass of the star to be much greater than the mass of the planet, we can use Kepler's Third law for the planet's orbit and solve for either a or T (since the mass of the star is so large, a is effectively equal to the planet's orbital radius). For example, if we consider the effect of Jupiter on

the sun:

Solving for a_* (using the fact that the mass of Jupiter is about 1000th of the Sun's mass), we have:

Thus, the displacement of the Sun due to Jupiter's gravitational field is roughly a solar radius. That's an incredibly small distance to measure! That's also why we measure velocity, instead of displacement, when searching for exoplanets.

Ringworlds

After Professor Johnson's very interesting plug for Professor Jason Wright's posts on Dyson spheres, I was reminded by a science fiction novel I started (and unfortunately, never got around to finishing) a long time ago: Ringworld, by Larry Niven.

When Freeman Dyson published his idea of a Dyson sphere many years ago, he postulated that any sufficiently advanced civilization would have to harness the energy of its host star to keep on growing. The reasons for constructing a Dyson sphere are simple: they provide immense amounts of energy, and the sphere itself provides a huge amount of room to live on. Imagine a surface 1 AU in radius, all available for habitation!

Artists' rendition of a Dyson sphere. Note that, unless there's another star in the system, the sphere probably won't appear lit (since it's enveloping the host star).

The problem with Dyson spheres is that it's very, very costly to construct a sphere with a radius of 1 AU! Think of all the raw material you would have to collect.

In Ringworld, author Larry Niven poses the question of a "partial" Dyson sphere - that is, taking only an equatorial slice of a Dyson sphere, a ring, and setting it in gravitational equilibrium around the star. The amount of living space would still be much greater than that of the Earth, due to the huge radius of the Ringworld, and the ring could be set to rotate to simulate gravity. Sufficiently efficient solar collectors could be placed throughout the Ringworld to power the entire system. An atmosphere could even be created, if the Ringworld could spin fast enough to prevent the atmosphere from escaping!

Artist's rendition of a Ringworld.

The novel itself is actually pretty good, and hopefully I'll get around to finishing it one day. Ringworld was the first novel to pose the idea of humanity (or any species), living on a ring rotating around the Sun. Could humanity one day build its own Ringworld to replace Earth, and live on free solar energy?

It turns out that this isn't the case, unfortunately. Although Dyson spheres, i.e. spherical shells, are gravitationally stable, the two-dimensional ring structure of a Ringworld makes it an inherently unstable equilibrium. Back to the drawing board, then.

The Phases of the Moon

Most people have looked up at the night sky and seen the moon. Sometimes, it looks like this:

Other times, it looks like this:

Sometimes, it even looks like it's not there!

Why does the moon behave so? What makes it look sometimes like a crescent, other times like a semi-round circle, and other times like a full circle or a dark spot? In this post I'll explain why the moon has phases, hopefully in a fashion that is clear and understandable.

To start off, we need a sense of our bearings. Below is a diagram showing the moon's position with respect to Earth:

The moon orbits around the Earth - every 27 days, it completes one revolution around the Earth and returns (more or less) to its original position relative to the Earth. By relative, I mean that from the Earth's viewpoint, the Moon is in its old position. Remember that the Earth rotates around the Sun, so Earth travels in an orbit around the Sun, with the Moon orbiting around the Earth at the same time.

What does this mean? Let's think about the we can see the Moon at night, first of all. The Moon is not a star - it doesn't produce light like the Sun (or else the night sky would be very bright!). Instead, the Moon reflects light produced from the Sun.

Now, imagine that the Moon is at the part of its orbit where it lies on a line in between the Sun and the Earth:

We can see that sunlight will strike the Moon's surface and reflect, indicated by the lighter shade of grey in the above diagram. However, we are located on Earth! As a result, the reflected moonlight will bounce back in the Sun's direction instead of towards us at the Earth. We can only see the dark side of the moon - in other words, nothing at all. This is called the new moon phase, where the moon is dark and we can't see it at night.

Armed with this knowledge, the other phases of the moon are relatively easy to understand. After the new moon phase comes the crescent moon phase. The moon then looks like a crescent in the sky - the moon isn't changing shape, however. Instead, the half of it that is illuminated shows up as a crescent from our point of view on Earth:

Next comes the full moon. As its name suggests, the full moon is when the moon is completely lit up - in other words, the half that is illuminated by the Sun is completely visible by us:

With knowledge of these three phases, we can understand the eight phases of the moon. A full chart is provided below:

Physically speaking, the phases are not particularly different from each other. At all times, about half the moon is lit up - the only thing changing is the fraction of the half that we can see from Earth. For example, the waxing crescent and waning gibbous phases are like inverses of each other - the half-circle shift in the position of the moon is what makes them look different.

So that's how the phases of the moon work. You may have noticed a few inconsistencies, though. For example: why can we even see the full moon? If the full moon occurs when the Earth is between it and the Sun, shouldn't the Earth block the light from the Sun, preventing it from reflecting it off the moon in the first place?

That's absolutely correct, and this happens during a lunar eclipse, when the full moon passes into Earth's shadow:

You may remark that lunar eclipses don't happen every 27 days! That's because the moon does not lie exactly on the same plane that the Earth and the Sun occupy. Instead, it lies on a slightly tilted plane:

The Earth doesn't orbit the Sun on the same plane as the moon orbits the Earth. Because of this, the full moon can occur. Every so often, however, the orbit of the moon lines up with the orbit of the Earth in just the right way so that the full moon happens when the Earth, Sun, and moon are all in the same plane. That's when we get a lunar eclipse.

As you can see, the phases of the moon are actually very simple if you take some time to think about it. With the simple step of abstracting your viewpoint to a spot outside of Earth, the phenomenon of moon phases becomes easy to understand.

The Time Scale of Star Formation and Stability

In this post I'll be doing #2 from this week's worksheet on star formation. The problem goes over deriving the time scale of star formation, and introduces the concept of the "Jeans Length." The question has multiple parts, which I'll do step by step.

The first part goes like this:

Consider a test particle in an e =  1 "orbit" around a point mass and use Kepler's Third Law to derive a general equation for the free-fall time. Frame this expression in terms of a single variable - the average density, p. What are the assumptions implicit in the last step? Are they valid?

 Let's begin by considering an e = 1 "orbit" (e = eccentricity) involving a the gas cloud (generalized as a point mass) and a test particle. In this case, we have an infinitely thin ellipse, essentially a straight line:

We can see that the total length of the "ellipse" is the radius of the cloud, R, which is twice the length of the ellipse's semimajor axis, a. Kepler's Law gives us the orbital period of a test particle traversing the ellipse, i.e. the time it takes for it to go back and forth on the line that is the ellipse:

where T is the orbital period, M is the mass of the cloud, and a is the semimajor axis.

We can see that the free-fall time, i.e. the time it takes for the test particle to move across the ellipse once, is half the orbital period. So, we have:

To put this expression in terms of density, we will use the following definition for a spherical gas cloud:

So, we have:

which gives us an expression for the time it takes for a self-gravitating cloud to collapse. We assumed a uniform density in the last step, which is valid, because the gas cloud is very diffuse, creating a near-uniform density throughout.

The second part of the question goes like this:

If the free-fall time of a cloud is significantly less than a "dynamical time," or the time it takes a pressure wave (sound wave with speed c_s) to traverse the cloud, the cloud will be unable to gravitationally collapse. Equate the free fall time to the sound crossing time and solve for the length variable R_j.

The time it takes for a sound wave to traverse the cloud (dynamical time) is given by the following:

If we equate the two times, we get the following expression for R_j:

which gives us an expression for the "Jeans Length," the subject matter of part three:

You have just performed an order of magnitude estimation of the "Jeans Length." A more careful derivation yields the following definition: 

 where c_s is the isothermal sound speed. Discuss the significance of this characteristic length.

The Jeans Length is intimately related to the collapse of a self-gravitating cloud of gas. When a cloud collapses, the edges of the cloud will create waves of pressure that traverse the cloud, opposing the gravitational self-collapsing force. If the pressure wave can reach the other edge of the cloud before the cloud collapses (i.e. in a time less than the free-fall time), then the cloud will stop collapsing. Thus, for clouds larger than the Jeans Length, the dynamical time (the time it takes for the pressure wave to traverse the cloud) will be larger than the free-fall time, and the cloud will collapse. On the other hand, for clouds smaller than the Jeans Length, the dynamical time will be smaller than the free-fall time, and the pressure waves will counteract gravity to prevent self-collapse.

Part four of the problem goes like this:

For simplicity, consider a spherical cloud collapsing isothermally with initial radius R_0 = R_j. Once the cloud radius reaches 0.5 R_0, by what fractional amount has R_j changed? What might this mean in terms of the number of stars forming within a collapsing molecular cloud?

From our above expression, we see that:

 So, if our initial radius halves in size, we have:

This tells us that the Jeans Length of the collapsing cloud decreases faster than the radius of the collapsing cloud.

What does this mean? If the Jeans Length is diminishing faster than the radius of the cloud, then the cloud will want to collapse faster and faster, since the difference between the Jeans Length and the radius is increasing. Because the density of the cloud is not perfectly uniform, smaller regions within the cloud that have higher density will therefore undergo their own gravitational collapse. This results in fragmentation, the process by which a large gas cloud fragments into smaller clouds that collapse into star clusters. (Note: the Jeans instability assumes an adiabatic contraction of the cloud, i.e. the temperature remains constant. This is not true in actuality).

The Spatial Scale of Star Formation

In this post I'll be doing #1 from this week's worksheet on star formation. The question itself is not that difficult, but its brief order of magnitude calculations give a good sense of the vast sizes involved in star formation. Here's the problem:

The size of a modest star forming molecular cloud, like the Taurus region, is about 30 pc. The size of a typical star is, to an order of magnitude, the size of the Sun:

a) If you let the size of your body represent the size of the star forming complex, how big would the forming stars be? Is there a biological structure in you that is roughly that size?

b) Within the Taurus complex there is roughly 3 x 10^4 solar masses of gas. To order of magnitude, what is the average density of the region? What is the average density of a typical star (use the Sun as a model)? How many orders of magnitude difference is this? Consider the difference between lead (11.34 g cm^-3) and air (0.0013 g cm^-3)

 Let's get some unit conversions first. we know that 1 parsec is about 200,000 AU, and 1 AU is about 100 solar radii. So, we have:

If we let the size of a star forming cloud to represent 1 body, we have:

Thus, the scaled size of a typical star is about 3 nanometers, which is about the diameter of a DNA helix.

Now, let's estimate the average density of the star-forming region. We will assume a spherical distribution of gas. The average density is given, then, by:

The mass of the cloud is about 3 x 10^4 solar masses:

The size of the cloud is 30 parsecs, so its radius is 15 parsecs:

Thus, the average density is:

The average density of a typical star, on the other hand, is:

The average densities are 21 orders of magnitude apart! Compared to the difference between lead and air (values given above), this difference is huge, highlighting just how sparsely distributed star-forming gas clouds are.

Equations of Stellar Structure

In this post I'll be deriving the relationships for stellar structure (i.e. the relationships between temperature, mass, density, pressure, and luminosity). We start with the equations for hydrostatic equilibrium, radiative diffusion, mass conservation, and the equation of state:

Next, we will derive the proportionality relationships for the above equations, using boundary conditions (i.e. mass of the star at radius R is the mass of the sun, temperature of the star at radius 0 is the central temperature, etc.). For this derivation, we will replace the differentials with deltas, i.e. "change," since we are only interested in proportionalities.
For the first equation, we have:

i.e. Pressure is proportional to the mass of the star times the density, divided by the radius of the star.

We will skip the second equation (radiative diffusion) for now. The third equation gives us:

i.e. The mass of the star is proportional to its radius cubed multiplied by the density.

The fourth equation gives us:

i.e. Temperature is proportional to pressure divided by density.

Let's combine our results to get a useful relation for the central temperature of a star. We know that:

where M is the mass of the star and a R is the radius of the star.

Using our results, we have:

Thus, the central temperature of a star is proportional to its mass divided by its radius.

Now we will derive the relations of stellar structure for a star on the main sequence (i.e. a star steadily fusing hydrogen, implying a constant core temperature T_c = constant).

For the mass/radius relationship, we have:

Hence, a star on the main sequence has a radius proportional to its mass.

To derive the luminosity/mass relationships, we look back at our radiative diffusion equation, and find that:

For a medium-mass star, we take kappa to be constant (this is because electron scattering plays the dominant role in determining the value of kappa, making is essentially constant). Hence:

Thus, the luminosity of a medium-mass star scales with the third power of its mass.

For a low-mass star, kappa is no longer constant. Instead, we have:

So, the luminosity/mass relationship becomes:

Thus, the luminosity of a low-mass star scales with the fifth power of its mass.

Now we will find the relationship between luminosity and temperature (effective temperature, not the temperature of the core).

For a medium-mass star, we have:

We also know that luminosity is related to radius and temperature by the following:

Hence, we have:

This is the luminosity/temperature relationship for a medium-mass star.

For a low-mass star, we have:

This gives us the Hertzsprung-Russell (HR) diagram: if we plot luminosity versus temperature on a log-log graph, we have:

i.e. a the log-log plot is linear. (for low-mass stars, the plot is also linear, with a gentler slope)

The HR diagram looks something like this:

Here is an actual HR diagram, using empirical data. You can see that for stars on the main sequence, the luminosity/temperature relationship is (roughly) linear on a log-log scale: