Hydrostatic Equilibrium

In this post I'll be doing problem #2 from this week's worksheet on Hydrostatic Equilibrium. I chose this problem because it goes through the derivation of hydrostatic equilibrium, which explains why the Sun is stable, a key concept in astrophysics. The question, essentially, is to explain what keeps the Sun from collapsing from gravitational forces.

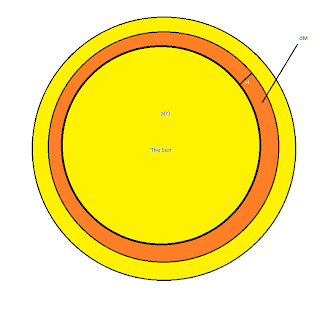
Let's start with assumptions. We can assume the Sun is a spherical cloud of gas - the Sun is mainly hydrogen and helium and is roughly spherical, so this assumption is valid. To solve this problem, we need to consider a "shell" of gas inside the sun of infinitely small thickness dr:

The mass, dM, in this shell, is given by the following expression:

where p(r) is the mass density of the Sun as a function of radial distance from the center.

Next, we will consider the gravitational force on this shell. There is no force on the parts of the Sun outside of the shell, since the Sun is spherically symmetrical, and a spherical shell exerts no gravitational force inside itself. Thus, the gravitational force on the shell is due solely to the fraction of the Sun within it. Since this portion is also spherical, we can use Newton's Law of Gravity and treat the interior as a point mass:

where M(r) is the total mass of the part of the Sun interior to the shell as a function of radial distance.

Now, we know the Sun is stable, i.e. its size is not changing very rapidly (if it is collapsing due to gravity, then we can't solve for a mechanism that prevents this gravitational collapse...). So, for the Sun to be (relatively) stable, there must be a force equal and opposite to the gravitational force on an arbitrary shell inside the Sun (i.e. every infinitely thin shell in the Sun has no net force on it). Now, the most likely candidate for the force is pressure, due to the gaseous composition of the Sun. So, we assume there exists a pressure force equal and opposite to the gravitational force:

We can also express the pressure force on a thin shell in terms of pressure (as a function of radial distance), from the definition of pressure:

Equating the two, we now have:

Or:

This is the equation for hydrostatic equilibrium in the Sun. In other words, the differential change in pressure as a function of radial distance from the center is proportional to the mass of the portion of the Sun within a sphere interior to the radius multiplied by the density at that radius, divided by the radius squared. This is the mathematical form of the mechanism that keeps the Sun from collapsing due to gravity.